How to use Option Greeks in Trading

Introduction to Option Greeks

Option Greeks are financial risk metrics that help traders assess how sensitive an option’s price is to the price of the underlying or some other risk factor. Mastering the Option Greeks is crucial for achieving success in options trading. Options trading goes beyond merely predicting market trends or direction; it involves grasping the factors that affect your option’s price. Knowing how to use Option Greeks can make or break your options trading success. This is where Option Greeks are essential. In this blog, we will clearly explain the five main Greeks (Delta, Theta, Vega, Gamma, and Rho) and also show you how to leverage each one of them to your trading profits while managing the risks involved.

Delta (Δ):

Option Greeks ‘Delta’ measures the sensitivity of option price based on changes in the underlying price. Delta of an option quantifies the expected change in an option’s price when the underlying asset’s price increases or decreases by ₹1, indicating the option’s directional sensitivity.

Point to Note:

• Call Option Delta: Varies between 0 and 1
• Put Option Delta: Varies between -1 and 0

Understanding the Option Greeks – Delta

Delta is calculated using some mathematical models such as the Black-Scholes model. Though the formula is very complex, traders can use any option trading platform to find delta values.

For example: Suppose a call option on Nifty 50 has a delta of 0.6, with a ₹1 increase in Nifty 50 resulting in a ₹0.60 rise in the option’s price.

Impact on Trade Profitability

• A high delta suggests that the option’s price will closely follow the underlying price change, which will help a trader to capitalize on significant price movements.
• Delta Hedging: Traders may use Delta to protect their positions or portfolios. For example, with a call option delta of 0.6, one may go short 60 shares (assuming a lot size of 100 shares) to achieve a delta-neutral position.

Risks and Optimization

Risks: Delta will always fluctuate as the underlying asset’s price changes, particularly for options nearing expiration.

Optimization: Traders can tweak their positions by adding or removing the number of contracts to maintain desired delta exposure, ensuring their strategy is aligned with market direction.

You may refer to the Podcast below on Delta:

Theta (Θ):

Option Greeks ‘Theta’ measures how much an option’s price will decrease over time, assuming all other factors remain constant. This is also known as ‘time decay’ in option trading. It is expressed as a negative value since options lose value as they approach expiration.

Understanding Option Greeks – Theta

The calculation is simple, theta represents the rate at which the option’s price loses value each day. For example, if an option has a theta of -0.05, it will lose ₹0.05 in value every passing day.
For example: If the TCS call option has a theta of -0.05, it will decrease by ₹0.05 every day, reducing its value over time.

Impact on Trade Profitability

• Option buyers must know that time decay works against them, especially near to the expiry.
• Option sellers, on the other hand, benefit from time decay as the option’s value decays, allowing them to profit from the premium collected.

Risks and Optimization

Risks: Days-to-Expiry (DTE). Theta accelerates as expiration approaches, making it crucial for option buyers to be careful of holding positions too close to expiration.

Optimization: To take advantage of theta, a trader can sell an option, such as in a covered call, credit spread strategy, or even naked Call/Put, to capture the premium as the option decays.

You may refer to the Podcast below on Theta:

Vega (ν):

Option Greeks ‘Vega’ measures how sensitive an option’s price is to changes in the volatility of the underlying asset. Higher volatility increases the likelihood of the option expiring in-the-money (ITM), thus increasing the option’s price.

Understanding Option Greeks – Vega

Vega determines the change in an option’s price for every 1% change in implied volatility (IV). If an option has a Vega of 0.10, then a 1% increase in volatility will increase the option’s price by ₹0.10.

For example, a Nifty 50 option with a Vega of 0.10 will increase in value by ₹0.10 for each 1% increase in implied volatility.

Impact on Trade Profitability

• Option buyers benefit from high Vega because an increase in volatility will lead to higher option prices thereby making more profit.
• Option sellers, on the other hand, will face the risk of higher losses if volatility spikes unexpectedly.

Risks and Optimization

Risks: A high volatility can work against you based on your position. If the market becomes more stable you hold a long position and implied volatility drops then you will incur loss. However, if you hold a short position then you benefit from the drop in IV.

Optimization: To maximize profit, traders can employ strategies like straddles or strangles, which profit from high volatility. Conversely, traders anticipating stable conditions can sell options to capitalize on a decrease in implied volatility.

You may refer to the Podcast below on Vega:

Gamma (Γ):

Option Greeks ‘Gamma’ measures how much an option’s delta will change when the underlying asset’s price changes by ₹1. Gamma is highest for at-the-money (ATM) options and decreases as options move further in or out of the money.

Understanding Option Greeks – Gamma

Gamma indicates the acceleration of the delta. If an option has a delta of 0.5 and a gamma of 0.02, a ₹1 increase in the underlying asset will increase the delta to 0.52.
For example, A Bank Nifty option with a gamma of 0.02 will have its delta increased by 0.02 for every ₹1 increase in Bank Nifty price.

Impact on Trade Profitability

• High gamma means that the delta will change rapidly, which can lead to quick gains or losses.
• Gamma scalping: Some sophisticated traders use gamma to adjust their delta-neutral positions frequently and profit from volatility.

Risks and Optimization

Risks: Options with high gamma are more sensitive to price movements, which can be risky near expiration.

Optimization: Traders can adjust their positions by using a combination buy and sell strikes in various strategies like butterfly spreads etc. This will help to manage gamma exposure and smooth out the potential risk.

Rho (ρ):

Option Greeks ‘Rho’ measures how much an option’s price will change for a 1% change in interest rates. Although it is the least impactful of Option Greeks in most trading conditions, it becomes more relevant for longer-term options.

Understanding Option Greeks – Rho

Rho indicates the change in the option’s price for a 1% change in the risk-free interest rate. For instance, if an option has a rho of 0.05, a 1% increase in interest rates will increase the option’s price by ₹0.05. In all practical situations, risk-free interest rates do not change frequently.
For example, a TCS call option with a rho of 0.05 will gain ₹0.05 for every 1% increase in interest rates.

Impact on Trade Profitability

• Call options have positive rho, meaning their prices will increase when interest rates rise.
• Put options have negative rho, so their prices will decrease when interest rates rise.

Risks and Optimization

Risks: Rho is not a significant concern for short-term traders but can impact long-term options or strategies involving LEAPS (Long-term Equity Anticipation Securities).

Optimization: To manage rho exposure, traders can balance their portfolios with different option types and durations.

Key Takeaways for Option Greeks

• Using Delta: To profit from directional moves, monitor your delta exposure and adjust it according to your market view. For example, increased delta exposure will generate more profit if you’re confident in the market direction.
• Leveraging Theta: If you’re an option seller, take advantage of Theta by focusing on net credit strategies like credit spreads, which benefit from time decay. Option buyers should avoid holding positions close to expiration without a clear and quick market movement.
• Managing Vega: Be aware of market volatility. Buy options when you expect volatility to increase, and sell options when you anticipate that volatility will drop and the market to stay calm. Use range-bound strategies like iron condors, short strangle, etc. to benefit from drop in volatility.
• Optimizing Gamma: Use gamma to manage the risk of sudden price moves. Keep an eye on gamma near expiration, as high gamma can lead to rapid changes in delta. Strategies like ratio spreads can help control gamma exposure.
• Controlling Rho: Though less impactful, monitor Rho in environments with changing interest rates, especially for long-term options. Adjust your positions to manage the effect of interest rate changes on your portfolio.

Summary Table: Impact on Option Price with the Greeks:

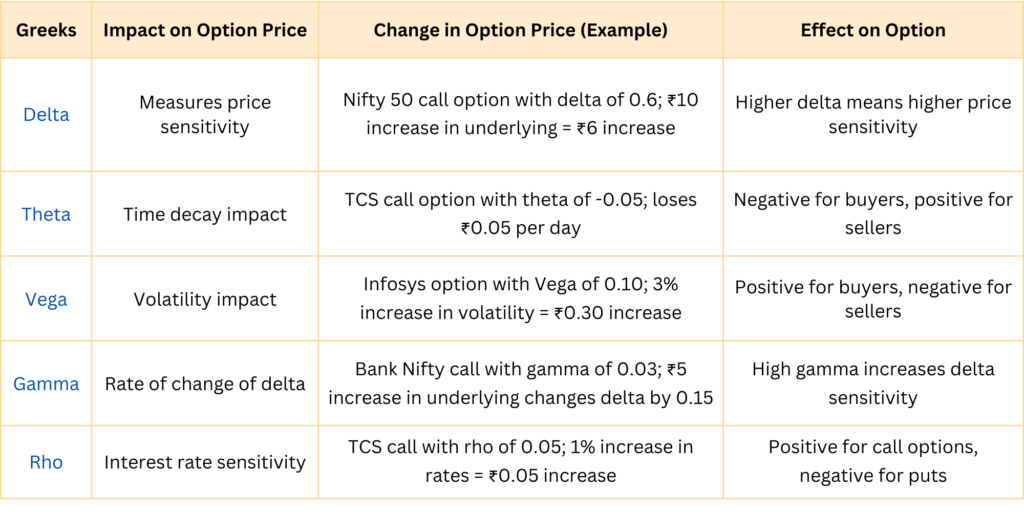
Conclusion

Each Greek plays a significant role in determining the price and behaviour of an option. By understanding how delta, theta, vega, gamma, and rho impact option prices, traders can make informed decisions, optimize their strategies, and better manage risk in the Indian stock market. This knowledge enables traders to anticipate how options will react to changes in the underlying asset’s price, time decay, volatility, and interest rates, ultimately enhancing their profitability and decision-making process.